
Optics
Optic basics - calculation of the optics
Tip:Online wizards for optical calculations can be found in the "Service" section.
Simplified optical beam path of a converging lens
Simple formulae can be used to calculate the appropriate optics. However, the calculated results are only approximate as they are based on a simple lens system (with one main plane).
Nevertheless, the simple calculations are usually accurate enough to calculate the working distance to within a few centimetres, depending on the field of view.

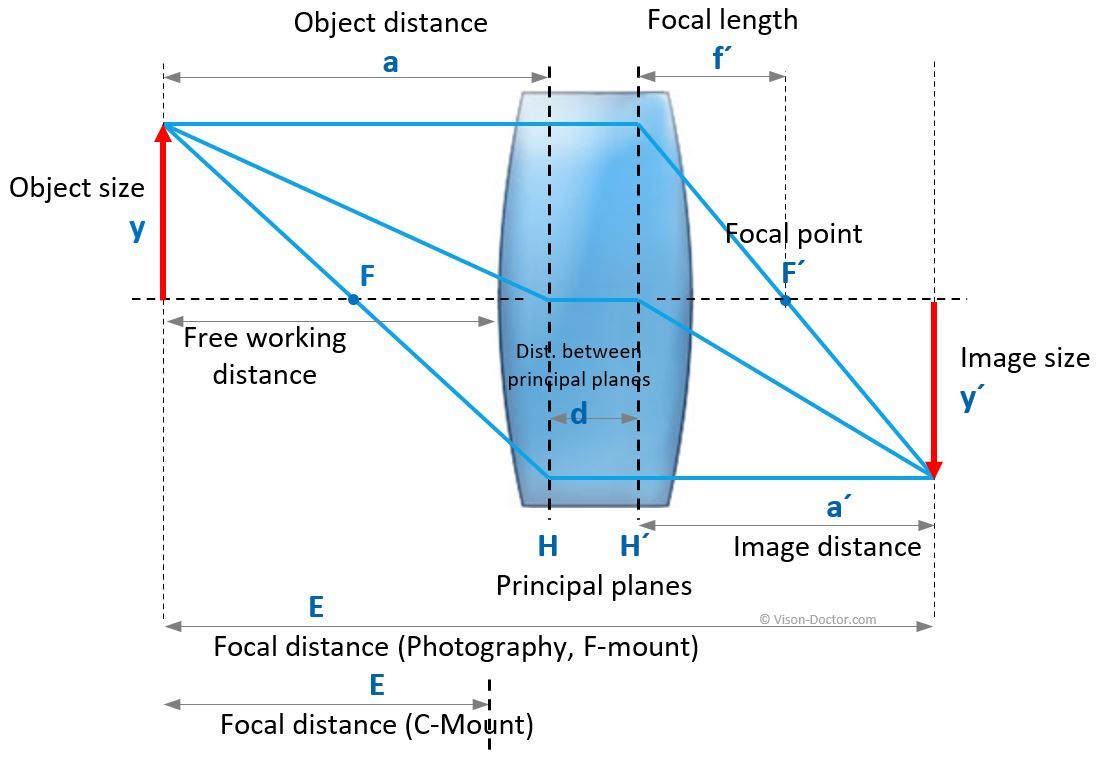
Optical beam path of a lens system
In practice, however, 4-7 lenses (groups) work together to produce the best possible image.
This complex lens system has two main planes, and the calculated object distance is the distance to the first main plane.
Strictly speaking, therefore, the object distance is not the 'working distance' to the front lens of the lens, but is usually somewhere in the optics. The calculation of the 'free working distance' to the front edge of the lens can only be accurately determined if the length of the optical system and the position of the main planes are known.
Often the user does not have this lens data, so a simple camera test is required or, in practice, a variable camera height adjustment of a few centimetres is planned.
The focusing distance of the scale on the lens is the distance to the mechanical front of the housing for C-mount lenses and the distance to the film plane for SLR lenses.
The most important parameters for the calculation are the object size, sensor size, working distance and focal length of the lens. However, the first two values are usually defined by the application, so that only the working distance for a specific focal length, or vice versa, has to be calculated.
The image size y´ - sensor size
The size of the image y´ is defined by the camera sensor, i.e. it must not be calculated most of the time. The measures are mostly given in inches, however, they are not real inch values but equivalents of historic tube cameras with an outer diameter of the glass tube of 1 inch.
1/1" 9,6 mm × 12,8 mm 16,0 mm (diagonal)
2/3" 6,6 mm × 8,8 mm 11,0 mm
1/1,8" 5,1 mm × 6,8 mm 8,5 mm
1/2" 4,8 mm × 6,4 mm 8,0 mm
1/3" 3,6 mm × 4,8 mm 6,0 mm
y´= y * f´ / ( a-f´ )
The object size y - object field
The object size y is usually the range to be detected which must be viewed by means of the camera. This value, too, is normally predefined and known, after all this is our test object with a little bit of surroundings.
An online wizard for the "calculation of the object size" can be found in the "Service" section.
y = y´ * (a / f' -1)
The focal length f´ - "lens type"
The focal length, measured in millimetres, is the distance between the optical centre of a lens and the focal point. All parallel incoming light rays intersect at this point. The focal length of an optical system depends on the optical power of the lens.
The focal length, f', is used to calculate the lens required and is therefore the most important specification to characterise an entocentric normal lens. The larger the value of the focal length, the greater the telephoto characteristics of the lens; small focal lengths represent wide-angle and fisheye lenses. In general, short focal length lenses tend to have more distortion than longer focal length lenses, but are usually more light intensive and compact. It is generally recommended to use a longer focal length when working at long distances.
An online wizard for the "calculation of the focal length" and other values can be found in the "Service" area.
f '= a / (y / y´ +1)
Example:
Which focal length is required in order to capture an image field of 150 mm when using a 1/2" sensor and 300 mm working distance?
y´ = 6.4 mm
y = 150 mm
a = 300 mm
f ' = 300 / ( 150 / 6,4 +1 ) = 12.3 mm
The focal length f' is 12.3 mm. In practice, lenses with a focal length of 12 mm or 12.5 mm are produced and marketed. In addition it is important to make sure that the lens meets the quality requirements of the sensor (standard optics, megapixel lens, colour-corrected optics, etc.) and whether the lens is capable of exposing the full size of the sensor. C-mount lenses, for example, are capable to expose at the maximum 1/2", 2/3" or 1" sensors, depending on the design. If the maximum image circle diameter of the optics is smaller than that of the sensor, strong image shading (vignetting) appears on the margin.
The object distance a - working distance
The object distance refers to the distance between the object (inspected part) and the centre of the optic lens groups. Unfortunately, the free working distance between the object and the front edge of the lens cannot be calculated without detailed knowledge of the lens design, but most of the time it is 2 - 3 centimetres lower.
An online wizard for the "calculation of the working distance" can be found in the "Service" area.
a = f' * ( y / y´ +1)
Example:
Which working distance is required in order to capture an object field of 100 mm using a 16 mm lens on a 1/3" camera?
y´ = 4.8 mm
y = 100 mm
f' = 16mm
a = 16mm * (100 mm / 4.8 mm +1)
a = 350mm
The image scale β
(also reproduction scale or magnification)
Usually no focal length is indicated for telecentric measuring lenses or macro-lenses, which would serve to calculate and select the optics. These lens types are characterised by the image scale β (beta). It can be calculated very easily.
An online wizard for the "calculation of the image scale" can be found in the "Service" area.
ß = y´ / y
Example:
A telecentric lens has the image scale β = 0.1. As a fraction this corresponds to 1/10. A camera with a 1/2" sensor and a size of 6.4 x 4.8 mm therefore serves to capture an object of 64 x 48 mm. If the same lens is used on a 1/3" camera, only 48 x 36 mm can be inspected.
The aperture angle 2w
Entocentric lenses have a fixed aperture angle. Therefore the object field to be viewed can be increased or reduced by increasing or reducing the working distance.
An online wizard for the "aperture angle " can be found in the "Service" area.
2w = 2 * arctan ( y´/ 2 * 1/f' ) (in rad)
If the aperture angle is very large, a strong distortion of the optics must usually be expected. Thus it is advisable for many applications to use a lens with a larger focal length and to increase the working distance instead in order to minimise the perspective (measuring) error.
On the other hand, extreme wide-angle optics (fisheye lenses as well as endoscopes) serve to solve special inspection tasks. In case of small working distances, the side of a part, a countersink or a bore can be inspected in this way.
Need to buy the perfect lens?
Vision-Doctor.com is a private, independent, non-commercial homepage project and not a technology provider or system integrator. Suitable technologies and further professional support can be obtained from the companies & partners listed below.
If necessary, I will be happy to provide a quick recommendation, contacts and brief information.















